Kinematics

Some basic observations

People walk. Insects fly. Fishes swim. Water flows. Top spins. Ringing bell vibrates. Wheel rotates.

Some special observations:

A person sitting in a moving bus finds the objects besides road as moving backward.

The speed and direction of rainfall changes as we run.

Geographical fact – earth rotates on its axis and revolves round the earth – we do not find it moving even an inch.

Most of the trains arrive at various stations at about the same time as mentioned in time table. How it does so?

 

Objective

Understanding these day-to-day phenomena and use the knowledge gained to apply in other fields to make our lives more easy and comfortable.

 

Syllabus

Motion in one dimension.

(Kinematics as the classification and comparison of motions.)

 

Assumptions

1. Motion is in straight line (vertical, horizontal or slant).
2. Moving object under observation is either particle (point object) or behaves like particle.

 

First thing first – concept of position and reference time

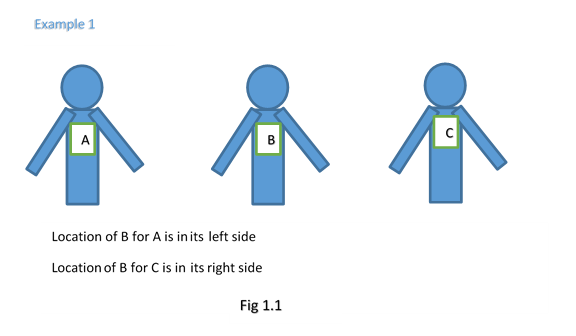
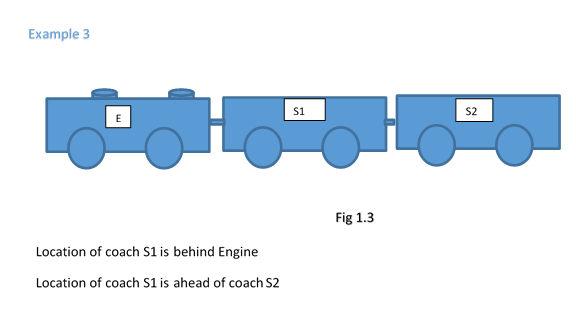
Position of an object is located with respect to a given body/point. This body/point is called reference point. It is also called as origin or zero point.

 

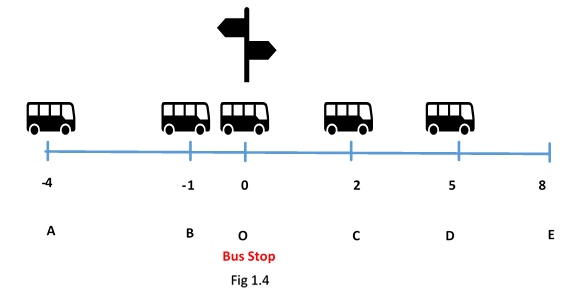
Now, let us consider the movement of a vehicle across a bus stop.

 

 

 

 

 

 

Things worth consideration here,

A body is in motion if it

• changes its position
• with respect to a given reference point
• with time

 

mathematically,

let the various positions on the straight road is represented as number line (X-axis). Various positions are marked as follows:

 

We explain this ‘change in position’ of a body as displacement.

 

Let, OA (x1) be the initial position and OB(x2) be the final position,

Then change in the position be,

Final position -initial position (Δx) = OB-OA

                = x2-x1

= -1 Km – (-4 Km)

                = -1 Km + 4 Km

                = + 3 Km, the positive sign represents the direction of positive x-coordinate (à)

 

Similarly,

Change in position (Δx) from B to D is OD -OB

                = x5-x2

= 5 – (-1)

                = 5+1

                = +6 Km (the positive sign represents the direction of positive x-coordinate (à)

 

For the for the entire journey,

The final position is OD and the initial one is OA. Thus, change in position will be

             OD – OA

            = x5-x1

=5 – (-4)

            = 5 + 4

            = 9 Km

 

 

 

 

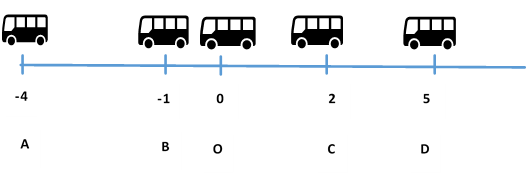
What if the vehicle has followed opposite path:

 

 

 

 

 

    

 

 

 

Displacement for the change in the position from D to C,

Final position -initial position (Δx) = OC-OD

                = x2-x1

= 2 Km – (5 Km)

                = 2 Km – 5 Km

                = – 3 Km, the negative sign represents the direction of negative x-coordinate (ß )

 

Similarly,

Change in position (Δx) from C to A is OA -OC

                = x5-x2

= -4 – (2)

                = -6 Km, the negative sign represents the direction of negative x-coordinate (ß )

 

Conclusion,

The mathematical sign for a positive displacement (change in position)
for a motion in straight line comes to be positive while that for a negative displacement comes to be negative.

 

 

Distance

Consider another situation when the bus in the first case (fig 1.4) moves to another point E and returns to D.

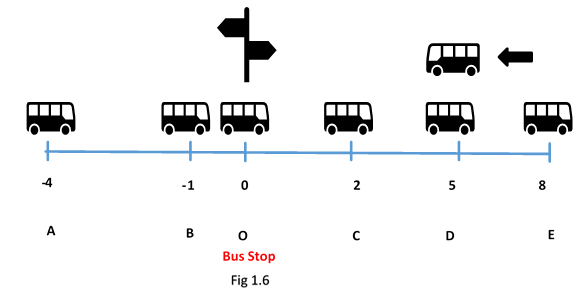
What is the displacement as the bus moves from A to E and then back to D.

The final position is OD and the initial one is OA. Thus, change in position will be

             OD – OA

            = 5 – (-4)

            = 5 + 4

            = 9 Km

We found that in both the situations (fig 1.4 and fig 1.6) the net displacement of the bus are of the same magnitude that is 9 Km. it means that the distance travelled by the bus from D to E and back to D have been not factored here.

This extra travel is reflected in distance.